Introduction
viscosity is one of the most important physical properties of a fluid.
It is the property that defines how easily or how slowly a fluid can flow in any medium. In simple words, viscosity represents the internal resistance (like friction) offered by a fluid to its own motion.
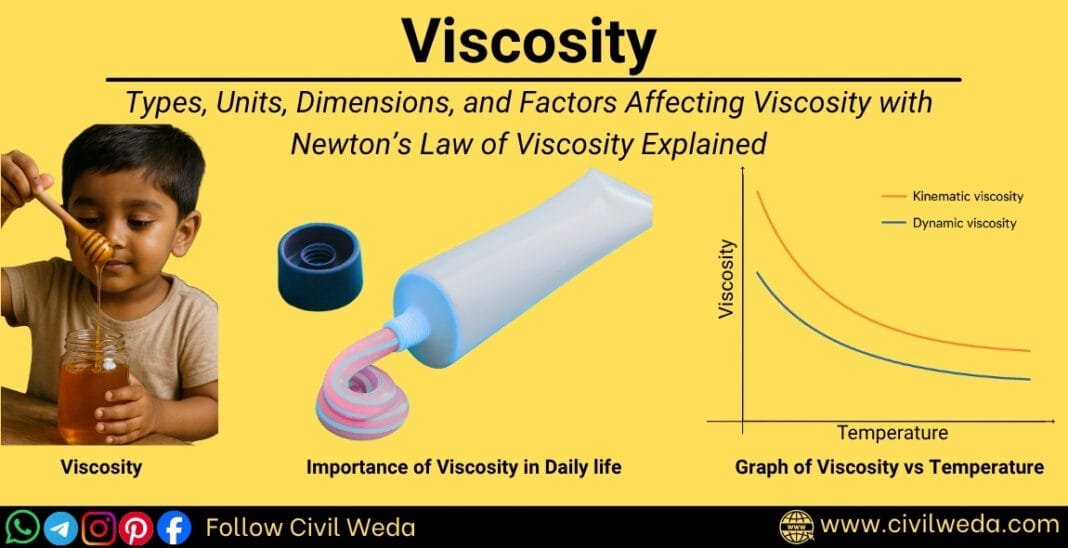
For example, when you pour honey and water, you will notice that honey flows much more slowly than water. This happens because honey has higher viscosity, while water has lower.
So, It helps us to understand why some fluids flow freely and others move sluggishly.
In civil engineering, the concept of viscosity is very important in the design of pipes, canals, pumps, turbines, and hydraulic structures, where the behavior of flowing fluids must be accurately predicted.
In this post, we will study the definition, types, formula, units, and importance of viscosity in daily life in a simple and easy-to-understand language which helps both semester exams and competitive exams.
So, let’s get started without any delay!
Definition of Viscosity
In Fluid mechanics, it is one of the most fundamental properties that help us study the behavior of real fluids. It represents the internal resistance offered by a fluid when one layer moves over another under the influence of an external force.
When a fluid flows, its adjacent layers move at different velocities. The top layer moves faster, while the bottom layer, which is in contact with the boundary surface, moves more slowly due to friction. This difference in velocity creates shear stress between the layers, and the fluid opposes this relative motion – this opposition is called as viscosity.
In other words,
“Viscosity is the property of a fluid that resists the relative motion between its adjacent layers due to internal friction.” Thus, it acts as a measure of the ‘stickiness’ or ‘thickness’ of a fluid. A highly viscous fluid flows slowly (like honey or engine oil), whereas a fluid with low viscosity flows easily (like water or air).
Read the detailed explanation of bitumen waterproofing in civil engineering by clicking here.
Newton’s law of viscosity

As per Newton’s law of viscosity, shear stress is directly proportional to the rate of change of velocity, or (velocity gradient). The relationship between shear stress and rate of shear deformation (velocity gradient) is given by:
τ = μ (du/dy)
Where:
- τ = Shear stress (N/m² or Pa)
- μ = Dynamic viscosity of the fluid (N·s/m² or Pa·s)
- du/dy = Velocity gradient perpendicular to the direction of flow (s⁻¹)
The constant of proportionality, μ, is known as the coefficient of viscosity or dynamic viscosity.
Facts to Remember:
- For ideal fluids, viscosity = 0 (they offer no resistance to motion).
- For real fluids, viscosity > 0 (they always resist motion).
- The SI unit of viscosity is N·s/m² or Pa·s.
- The CGS unit of viscosity is Poise (P).
- 1 Poise = 0.1 N·s/m²
So, we can say that it is not just a theoretical concept – it plays a major role in understanding how fluids move in pipes, channels, turbines, and lubrication systems, which are all essential parts of civil engineering hydraulics.
Types of Viscosity
Viscosity is the internal frictional resistance offered by a fluid when it flows. Depending on how it is measured, viscosity is expressed in two forms: one is dynamic viscosity, and the other is kinematic viscosity. Both types are interrelated but have different physical meanings and applications in fluid mechanics.
Dynamic Viscosity (μ)
Dynamic viscosity is defined as the shear stress required to produce a unit rate of angular deformation (velocity gradient) when the fluid is under laminar flow conditions. It is also known as absolute viscosity. In general, it determines how much tangential force is required to make one layer of fluid slide over another with a unit velocity gradient. It depends mainly on: Temperature, Pressure, nature of the fluid, etc.
Mathematically,
τ=μ (du/dy)
Where:
- τ = Shear stress (N/m² or Pa)
- μ = Dynamic viscosity of the fluid (N·s/m² or Pa·s)
- du/dy = Velocity gradient perpendicular to the direction of flow (s⁻¹)
This equation is derived from Newton’s Law of Viscosity; hence, fluids that follow this relationship are called Newtonian fluids.
Facts to Remember:
- SI Unit of Dynamic Viscosity: N·s/m² or Pa·s
- CGS Unit Dynamic Viscosity: Poise
- Dimension Dynamic Viscosity: [M¹L⁻¹T⁻¹]
Kinematic Viscosity (v)
Kinematic viscosity is defined as the ratio of dynamic viscosity (μ) to the density (ρ) of the fluid. It represents the ability of a fluid to flow under its own weight (without any external force).
Mathematically,
Kinematic viscosity (v) = μ /ρ
Where,
- ρ = density og fluid
- v = Kinematic Viscosity
- μ = Dynamic viscosity (N·s/m² or Pa·s)
Facts to Remember:
- SI Unit of Kinematic viscosity: m²/s
- CGS Unit of Kinematic viscosity: Stoke
- Dimension of Kinematic viscosity: [L²T⁻¹]
Comparison Between Dynamic and Kinematic Viscosity
A quick comparison between dynamic and kinematic viscosity is given in table below:
| Property | Dynamic Viscosity (μ) | Kinematic Viscosity (ν) |
| Definition | It is the internal resistance offered by a fluid when one layer moves over another under the action of an external force. | It is the ratio of dynamic viscosity (μ) to the density (ρ) of the fluid. |
| Formula | τ = μ × (du/dy) | ν = μ / ρ |
| Physical Meaning | Measures the internal friction between moving layers of a fluid. | Measures the resistance of a fluid to flow under its own weight (momentum diffusivity). |
| Dependency | Depends mainly on temperature. (For liquids → decreases with temperature, for gases → increases.) | Depends on both the temperature and density of the fluid. |
| SI Unit | N·s/m² or Pa·s | m²/s |
| CGS Unit | Poise (P) | Stoke (St) |
| Conversion | 1 P = 0.1 N·s/m² | 1 St = 10⁻⁴ m²/s |
| Dimension | [M¹ L⁻¹ T⁻¹] | [L² T⁻¹] |
| Typical Range | 10⁻³ – 10² Pa·s | 10⁻⁶ – 10⁻³ m²/s |
| Use in Fluid Mechanics | Used in evaluating shear stress, pressure drop, and energy loss due to friction. | Used in Reynolds number, flow classification, and hydraulic design calculations. |
Factors Affecting on Viscosity
The viscosity of a fluid does not remain constant. It varies with changes in temperature, pressure, density, impurities, and molecular structure of matter. These variations affect both dynamic viscosity (μ) and kinematic viscosity (ν) differently.
Understanding these factors is essential for civil engineers because viscosity directly influences fluid flow, head loss, Reynolds number, and hydraulic design efficiency.
Understanding of these factors is essential for civil engineers because viscosity directly influences fluid flow, head loss, Reynolds number, and hydraulic design efficiency.
Let’s discuss each factor in detail 👇
Effect of Temperature
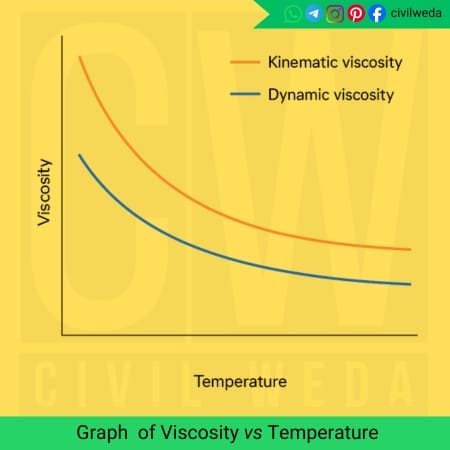
Temperature is the most dominant factor that influences viscosity. It affects the strength of molecular cohesion and momentum transfer within the fluid.
In the case of a liquid, when we increase the temperature of a liquid, it reduces the internal resistance of the liquid, which decreases its dynamic viscosity, but increases the kinematic viscosity of the liquid.
In the case of a gas, when we increase the temperature of a gas, it increases the dynamic viscosity of the gas because at higher temperatures, the molecular velocity and collision frequency increase, which causes more momentum transfer between gas layers, thus increasing the dynamic viscosity and also the kinematic viscosity of the gas.
Some common fluids and their viscosity variation with temperature are shown in the table below:
| Fluid | Temperature | μ (Pa·s) |
| Water | 20°C | 1.002 × 10⁻³ |
| Water | 40°C | 0.653 × 10⁻³ |
| Air | 0°C | 1.71 × 10⁻⁵ |
| Air | 100°C | 2.08 × 10⁻⁵ |
Effect of Pressure
The effect of pressure on viscosity is relatively small compared to temperature, but it still plays a noticeable role in some fluids, especially at high pressures.
In the case of a liquid, when we increase the pressure of a liquid, its dynamic viscosity increases slightly because at higher pressure, it forces the molecules closer together, increasing the intermolecular attraction and internal friction within the liquid. As a result, the resistance to flow becomes slightly higher at high pressure in the liquid.
In the case of gas, the effect of pressure on dynamic viscosity is very small under normal conditions. At moderate pressures, μ remains almost constant, but at very high pressures, molecular collisions become more frequent, causing a slight increase in the viscosity of the gas.
Effect of Density
The density of a fluid plays an indirect but important role in determining its kinematic viscosity (ν), while it has almost no direct effect on dynamic viscosity (μ), but with the help of density, we calculate the kinematic viscosity. Density shows an inverse relation with kinematic viscosity.
Kinematic viscosity =μ /ρ
Some other common physical parameters that affect the viscosity of liquids and gases are given in the table below:
| Factor | Liquids | Gases | ||
| Dynamic (μ) | Kinematic (ν) | Dynamic (μ) | Kinematic (ν) | |
| Temperature | Decreases with an increase in temperature | Increases with an increase in temperature | Increases with an increase in temperature | Increases with an increase in temperature |
| Pressure | Slightly increases with pressure | Slightly decreases with pressure | Almost constant (slight increase at high pressure) | Slightly decreases |
| Density (ρ) | Almost no effect | Inversely proportional (↑ρ → ↓ν) | No direct effect | Inversely proportional (↑ρ → ↓ν) |
| Impurities / Additives | Increases (due to higher internal friction) | Increases | Negligible or slight increase | Negligible |
| Molecular Structure | Complex or long-chain molecules → higher μ | Complex or long-chain molecules → higher ν | Simple, small molecules → lower μ | Simple, small molecules → lower ν |
Measurement of Viscosity
The viscosity of a fluid is generally measured by determining the resistance offered by the fluid to flow or by observing the rate at which a fluid layer moves under a given force. For this purpose, different instruments known as viscometers or viscosity meters are used.
Each type of viscometer is based on a specific physical principle and is suitable for particular kinds of fluids. I will explain it in our other post. If you want to read more about it in detail, you can check this article.
Importance of Viscosity in Civil Engineering

In civil engineering, viscosity plays a vital role in understanding how fluids behave when they flow through pipes, channels, and hydraulic machines. It influences the energy loss, discharge rate, lubrication, and sediment transport, making it one of the most important fluid properties in the design and analysis of hydraulic structures.
Read more Civil Engg topics
- Chlorination of water
- Per Capita Water Demand
- Pile foundation
- Drip Irrigation
- Instrument used in a chain survey
- Fillet Weld
- Bulking of sand
- Instrument used in a chain survey
Conclusion
Viscosity is one of the most significant properties of fluids that defines their resistance to flow. It governs how easily a fluid can move, how much energy is lost due to internal friction, and how efficiently mechanical systems and hydraulic structures operate.
In this post, we discussed the complete concept of viscosity, including its definition, types, units, factors affecting it, and its importance in civil engineering applications. We also learned two types of viscosity: Dynamic viscosity and Kinematic viscosity
Both these properties are essential for fluid flow analysis, hydraulic design. It helps civil engineers to design efficient systems such as pipelines, canals, turbines, pumps, and treatment plants where fluid motion plays a vital role. Without proper consideration of viscosity, the prediction of flow behavior, head loss, and energy consumption can become inaccurate.
Hence, it is not just a theoretical concept; it is a practical engineering parameter that ensures safety, economy, and efficiency in every hydraulic structure.
If you wish to study how viscosity is measured experimentally using different viscometers and methods, you can comment in this post.
FAQs on viscosity
What is viscosity in fluid mechanics?
Viscosity is the property of a fluid that defines its internal resistance to flow. It determines how easily one layer of fluid can move over another. High-viscosity fluids (like oil or honey) flow slowly, while low-viscosity fluids (like water or air) flow easily
What is the SI unit of viscosity?
Dynamic viscosity (μ): N·s/m² or Pa·s
Kinematic viscosity (ν): m²/s
What is the viscosity of water at 20°C?
At 20°C,
Dynamic viscosity (μ) = 1.002 × 10⁻³ Pa·s
Kinematic viscosity (ν) = 1.004 × 10⁻⁶ m²/s
What are viscometers used for?
Viscometers are instruments used to measure the viscosity of a fluid. Different types include Ostwald, Redwood, Hoppler, and Brookfield viscometers, each designed for specific types of fluids and applications.
How does temperature affect viscosity?
In the case of liquids, viscosity decreases with an increase in temperature. And in the case of gases, viscosity increases with an increase in temperature.
Thank You for Reading! 🙏
We hope this article helped you clearly understand the Viscosity in civil engineering. If you found this complete article useful, please share it with your friends and university students. For more informative posts on civil engineering topics, stay connected with Civil Weda. 🚀